Philosophie + mehr: Das Alter der Welt + Imaginäres Gespräch über künstliche Intelligenz
Widerlegung der Punktrechenregel (fehlende Symmetrie)
Neue Kategorie: Witze [ausschließlich für Absolventen dieser Seite] | DEUTSCH GERMAN [ENGLISH: scroll down; => already translated] Logik des Formalismus1. Subtraktion 2. Negation 3. Cantor 4. Beweis 5. Cantor 3 (+ Austausch mit Wilfrid Hodges) 6. Boole 1 7. IF2 8. Boole 2 9. Reform Σ Π Θ [noch fertigzustellen] 10. Wurzelfunktion 11. Binome [Artikel `lebt´ noch] 12. Euler 13. Drehmoment und Quadratwurzelfunktion 14. Master and Slave 14.05.2024 [27. Sept. 2024 abschließend korrigiert] Master and Slave — ist die Bijektion definiert über `Surjektion und Injektion´? 1. Subtraktion [Änderung S. 1, 12.07.2020] • Die Definition des mathematischen Körpers, die Grundlage einer Algebra, ist nur dann widerspruchsfrei und somit gültig, wenn die rückwärts gerichtete (die degressive) Strichrechnung (die Subtraktion) ausgeschlossen wird. Behauptung: Subtraktion ist nicht Addition des inversen Elementes. Beweis: Subtraktion (10 Seiten DIN A 4) Korrektur: Seite 8, Absatz 2: worüber die Subtraktion ... in der Wirkung ausdrückt ... => worüber die Subtraktion ... in der Wirkung ausgedrückt ...
2. Negation • Über die Definition des mathematischen Körpers gilt die inverse Verknüpfung als ausgeschlossen. Behauptung: Objekt und Verknüpfung sind bezüglich Inversion intrinsisch. Beweis: Negation (5 Seiten DIN A 4)
3. Cantor • Der mathematische Körper wird als Menge im Sinne der Definition von Cantor bezeichnet. Behauptung: Elemente einer Menge sind untereinander gleich. Beweis: Cantor (3 Seiten DIN A 4) 4. Beweis • Cantor hat eine Behauptung aufgestellt; die sogenannte Kontinuumshypothese. Das Problem belegt einen Platz auf der Hilbert-Liste aus dem Jahre 1900. Behauptung: Die Potenzmengen-Staffelung ist per Definition inkonsistent und ungeeignet als Kriterium der Überabzählbarkeit. [Man bedenke: alle logischen Verbindungen von Elementen finden innerhalb der Menge der natürlichen Zahlen statt.] Beweis: Beweis (7 Seiten DIN A 4)
5. Cantor 3 (Korrektur S. 12, ehem. 5. `Kolumnenanzahl´) • Cantor´s zweites Diagonalargument ist Grundlage diverser Herleitungen. Es zu widerlegen wäre, als Ergänzung zu der Herleitung im Abschnitt `Beweis´ das endgültige Ende einer fatalen Fehlentwicklung des Faches. Als Konsequenz folgt, dass das zweite Diagonalargument im Widerspruch zum ersten Diagonalargument steht! Behauptung: Das zweite Diagonalargument ist ein Zirkelschluß, die Folgerungen nicht wahr. Beweis: Cantor 3 (12 Seiten DIN A 4)
Hodges vs Kepp ein kurzes, abgeschlossenes (?) Kapitel: ”An Editor Recalls Some Hopeless Papers” (Ein Redakteur / Herausgeber) erinnert einige hoffnungslose Arbeiten). Starker Tobak in der Überschrift sowie im Inhalt. Eine Abqualifizierung diverser Aufsätze, die von den jeweiligen Autoren als wissenschaftlich anerkennenswert eingestuft worden sind. Wilfried Hodges kommt lobenswerterweise ohne Nennung der Autoren aus. Da mir die `hoffnungslosen´ Arbeiten nicht vorlagen, habe ich Hodges persönlich angeschrieben und tatsächlich einen Austausch initiieren können. Ziel war selbstverständlich, seine Meinung zu Cantor´s zweitem Diagonalargument umzustimmen. Hodges hat selbstverständlich zugestimmt, dass der Stellentiefe ny einer Zeichenkette (deren Anzahl von Zeichen) die Anzahl 2^ny verschiedene Zeichenketten zuzuordnen ist, wenn die Basis der Stellenwerte zwei ist. Den Zusammenhang der Anzahl der verschiedenen Zeichenketten (µ bei Cantor) und der endlichen Anzahl der Zeichen dieser Ketten (ny bei Cantor) habe ich Hodges mehrfach ausführlich vorgetragen. Zuletzt:
Hodges hat mich legitimiert, seine abschließende Antwort zu diesem Komplex, unter Nennung seines Namens öffentlich zu machen.
Ich enthalte mich jedweder wertenden Aussage hierzu. Möge sich jeder selbst sein Urteil bilden. Ergänzend, unter Anwendung der Regeln aus der vorigen mail (Punkte 1 ... 3), der Nachweis der Vollständigkeit der Entwicklung von ny:
6. Boole 1 • Als Erfüllung eines Körpers begrenzt auf zwei Elemente wird unter anderem die Auslagenlogik von Boole angeführt.
Behauptung: Die Boolesche Auslagenlogik gehört nicht zu den Algebren. Beweis: Boole 1 (1 Seite DIN A 4)
7. IF 2 Behauptung: Die Definitionen des zwei-elementigen Körpers wider-sprechen den allgemein gültigen Axiomen eines Körpers. Beweis: IF2 (9 Seiten DIN A 4)
8. Boole 2 Behauptung: Die Boolesche Auslagenlogik ist nicht Körper konform. Beweis: Boole 2 (1 Seite DIN A 4)
9. Reform Σ Π Θ Behauptung: Die Definition einer Widerspruchsfreien Algebra ist möglich. Beweis: Reform Σ Π Θ
(demnächst hier frei als Volltext geplant) 10. Wurzelfunktion Behauptung: Die Operation des Radizierens ist neu zu definieren. Beweis: Wurzelfunktion Neu: ergänzt auf S. 2 und 3 (28.06.2020). Der Grundsatz dieser Ausführung ist über die Arbeit `Drehmoment und Quadratwurzel´ in englischer Fassung `double peer reviewed´ anerkannt (s. 13). 11. Binome Behauptung: Die Binome sind weder in Anzahl noch in Logik vollständig. Beweis: Binome (vorerst 3 Seiten DIN A 4)
12. Euler [Korrektur auf Seite 4, 03.05.2020 / S. 6, 08.05.2020] Behauptung: Der Euler-Äquivalenz fehlt jegliche logische Grundlage. Beweis: Euler (7 Seiten DIN A 4)
13. Drehmoment und Quadratwurzel • Mit den Wurzeln aus der Angabe zum Drehmoment lassen sich rückentwickelnd somit die Faktoren Kraft und Hebellänge bestimmen. Nach den Regeln 'plus mal plus gleich plus' und 'minus mal minus gleich plus' die beiden Möglichkeiten als Ursachen des linksdrehenden Moments. Es sei die Aufgabe, auf dieselbe Art (allein über die Wurzelfunktion) die Möglichkeiten für die Ursachen des rechtsdrehenden Moments zu bestimmen!
Veröffentlicht im 'European Scientific Journal', Ausgabe Vol. 9, Nr. 33, November 2013, Seite 179 ... 183. http://eujournal.org/index.php/esj/ weiterklicken über 'ARCHIVES' bzw.: http://eujournal.org/index.php/esj/issue/archive oder direkt: http://eujournal.org/index.php/esj/issue/view/103 (16-ter Artikel) Behauptung: Mit der Reform wird die Wurzel eindeutig, die Ergebnisse vollständig. Beweis: Paper, ESJ (5 Seiten DIN A 4)
14. Master and Slave
.....................................................................................................................
• ∀ ∃ ⊥ ∫ | ‰ ≤ ~ = ≠ ≡ ∨ Λ + ⋅ ∗ − : ÷ ⁄ √ Σ (Sigma - Summenmenge), Π (Pi - Produktmenge), Θ (Theta - Quotientmenge)
+ − ± ⋅ × ∗ : ÷ / < ≤ = ≠ ≡ ≥ > ∞ • 〈 〉
ENGLISH ENGLISH ENGLISH [`Frinton-translation´: "I´ll do my best." – If you find a mistake or some, please let me know.]
R real numbers I imaginary unit P prime numbers R.I.P. old mathematics, reform takes charge! Logic of formalism 1. Subtraction 2. Negation 3. Cantor 4. Proof 5. Cantor 3 6. Boole 1 7. IF2 8. Boole 2 9. Reform Σ Π Θ [to be done] 10. Square-root-function 11. Binoms [to be done] 12. Euler 13. Torque and Square-root-function 14. Master and Slave 1. Subtraction [corection — p. 5 — 2020/07/13] • The definition of the mathematic field, the foundation of an algebra, only then is without contradiction and valid by that, if the backwards orientated (the degressive one) of plus and minus (the subtraction) would be excluded. Assertion: Subtraction is not equal to Addition of the inverse Element. Proof: Subtraction
2. Negation • By the definition of the mathematic field the inverse combination is excluded by the prevailing opinion. Assertion: Object and Combination are intrinsic by Inversion. Proof: Negation
3. Cantor • The mathematic field so is called a set as it was in the mind of the definition of Cantor. Assertion: Elements of a set are equal one another. Proof: Cantor
4. Proof • Cantor elaborated an assertion; the so called Continuous-Hypothesis. The problem ranges at the first place of the Hilbert-List of the year 1900. Assertion: The Continuos-Hypothesis of Cantor gets proofed. Proof: Proof
5. Cantor 3 (corrected at page 12 (on columns) • Cantor´s second diagonalargument is basis for some conclusions. To disprove that, as a completion to the conclusion in part `proof (Beweis)´, would be the absolute end of a wrong development in that topic. As a consequence it follows that the second diagonal argument stays in contradiction to the first diagonal argument! Assertion: The second diagonalargument is a Circular argument, the conclusions are not valid. Proof: Cantor 3
6. Boole 1 • To fulfill a field, limited by two elements, amongst other things the Boolean (statement-) logic is quoted. Assertion: The Boolean (statement-) logic doesn´t belong to any algebra. Proof: Boole 1 (1 page DIN A 4) 7. IF 2 Assertion: The definitions of a field depending on two elements are staying in contradiction to the universal valid axioms of a field. Proof: IF2 (9 pages DIN A 4)
Supplement:
Page 8 of 9
Page 9 of 9 8. Boole 2 Assertion: The Boolean (statement-) logik isn´t conform to a field. Proof: Boole 2 (1 page DIN A 4) 10. Square-root-function Assertion: The operation of radiating has to be defined new. Proof: Square-root-function (3 pages DIN A 4) The principle of this examination get `double peer reviewed´ accepted by the paper `Torque and Square-root-function´ (see 13). New: extended at page 2 and 3. 12. Euler Assertion: The Euler-Equivalence doesn’t have a logical foundation. Proof: Euler (8 pages DIN A 4)
13. Torque and square-root-function 'Force on y-axis´ and `lever-length on x-axis´ makes – for the product – `torque for z-axis´. Comprehensible left-turning torque by: force = pos. y-value and: lever-length = pos. x-value.
Right so left-turning torque at: force = neg. y-value and: lever-length = neg. x-value.
By the roots of the nomination to the torque the factors force and lever-length are determineable. Following the rules `plus times plus equal plus´ and `minus times minus equal plus´ the two possibilities as reasons for the left turning torque. It should be the exercise to determine the reasons for the right-turning torque in the same art (only by the root-function)!
Published at `European Scientific Journal, vol.9, No. 33, november 2013, page 179 ... 183. http://eujournal.org/index.php/esj / click at 'ARCHIVES' or.: http://eujournal.org/index.php/esj/issue/archive or direct: http://eujournal.org/index.php/esj/issue/view/103 (16-th article) ................................................................................................................................
14. Master and Slave
Boolean algebra (older/preparing version)
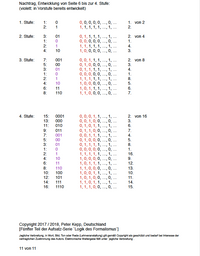
In the Boolean algebra the symbols of logical OR and logical AND are used. By them the symbols 0 and 1 are combined. As result again only the symbols 0 and 1 are offered exclusively. But logical OR as well as logical AND are no combinations. Where the disagreement is located? The so called tabulations of truth: (OR ≡ ∨, AND ≡ Λ ): 0 ∨ 0 = 0 0 ∨ 1 = 1 1 ∨ 0 = 1 1 ∨ 1 = 1 0 Λ 0 = 0 0 Λ 1 = 0 1 Λ 0 = 0 1 Λ 1 = 1 seem to be understandable. But do we really understand them? Even the assumption from the depiction in form of a chart to the usual form of a mathematical equation, which is carried out here, should have been proofed, for that the sense of the Boolean algebra will not be circumvented. To make a rash action with reference to the digital calculation makes no sense. Because firstly there the expressions which are handled consists on chain of any length of digital symbol and secondly in the Boolean algebra there is no representation of the amount which has to be carried over. But a carryover strictly is neccessary to combine two expressions set-theoretical in an algebraic way. In digital-technics beneath the possibilities to give OR or AND between the two expressions essentially the addition is used. By a `complete-adder´ the carryover is calculated and the next higher position in the line of expression is given or rather predefined. A genuine combination requires the openess coming with the possibility by that the solution of the combination may be different to the source-expressions. At restriction on digital values of source-expressions and solutions the openess only consists in the carryover of the solution, which determines the next higher position in the line of expression. One could depict the logical AND of the Boolean algebra on the minimum-function and the logical OR on the maximum-function. But both would be functions, no combinations!
A detailed treatment of this subject is planned for the print-version / the book `Logik des Formalismus´ (logic of formalism). ................................................................................................................................
Euler-equivalence
Beneth the fact by that the imaginary unit is ceased to apply in the developement of the Euler-equivalence there are more miss-assumptions.
> Addition of the not-commensurable parts of the complex expression of the developement of the series.
> Two-dimensional exponent (angle)
> Assumption of dimensional-strange links of the series
> Double change of the angle by the mass of arc
To the two-dimensional exponent: What results if we take the 114.6... degree-of-angle - root of four? Plus-minus two of course, if one follows the expert opinion (e.o.) (!). Angle as exponent of root? If one wants to follow Euler, yes. The angle by mass of arc of course, because that should be able by the Euler-equivalence (exp(iφ)).
To take the nth root is the inverse function to the exponentiation.
From a exp(b) = c follows: b´th root from c results to plus-minus a (e.o. at b = 2). And the angle of 114.6...° comes therefore: two (arc) is to π as the searched arc to 180° (114.6...° = 180° * 2/π). But the angle is a two-dimensional definition after all – no matter in what form of expression, mass of arc or degree; you may object now – surely you are right!
First to the sceptics, fivetimes the possibility, to analyse the standpoint of the expert opinion (e^ix = cos x + i sin x):
1. Physics / square of a unit At the developement of the series of the complex e-function the imaginary unit is developed too by all the powers of the natural numbers.
Is there an example in which the square of the unit, not that of the mass, is defined?
2. Mathematics / depicting by coordinates In the area of complex numbers the x-axis-segment and the y-axis-segment are standing for the coordinates of the complex number.
Is it allowed to show these coordinates as beeing able to be combined by addition? If yes, how could that be established?
3. Mathematics / developement of the unit In the area of complex numbers the x-axis stays for the real part (Re). By the logic of mathematics without mass. The should have been written included by squared brackets; the unit, as an expression of language, has to follow. A value would be combined by number, mass and unit. Without mass, with free determinable number x , a value of the real axis should be written as `x[{ }] Re´ (`[{ }]´ stays for emty set). That means, not the more times of a smallest part of the real unit is named by the worth of number of the x-axis. The number (as beeing accompanied Re) stays for the worth of number or together for the worth of number and mass, by the way of interpretation. [By f(x) = x^2 + x +1 doesn´t follow the square of the unit by x^2 , but only of the number x ! Otherwise x^2 and x couldn´t be added (square plus length!).] For the imaginary part of the complex number it is valid to be free of mass as it is for the real part. A value of the y-axis correctly should have been written as `y [{ }] Im´. The functional, raising to power developement of the value y^2 should be restricted to have consequence only to any number for y !
Why didn´t Euler and following all the mathematicians (and physicists) keep this logical guideline? Why, in the formulation of the series of isin x , the unit `i´ is been putted as a factor of the function and too is still been developed?
4. Mathematics / addition of inkommensurable (unit-strange) series In the area of complex numbers the values of the x-axis are unit-strange to thatone of the y-axis; they are, by definition, not addable – they are incommensurable.
sin x = x^1/1! – x^3/3! + x^5/5! – + ...
e^(iφ) = (1 – φ^2/2! + φ^4/4! – + ...) + i (φ^1/1! – φ^3/3! + φ^5/5! – + ...) [φ im Bogenmaß]
Why at the Eulerequivalence [complex number C = f(e^(iφ), φ); depicted by coordinates] the series to the real part (x-axis stays for Re => x = cos φ) is addable to that one of the imaginary part (y-axis stays for Im => y = sin φ)?
5. Mathematics / e^x > module (sinx, cosx) ; x > 0 How the module of `cos x + sin x´ , [ |sqrt(cos^2 x + sin^2 x)|; amount of the square-root of the sum of the squares of sin and cos ] which always is equal one, could amount to a very quick growing function `e^x´ , if the y-axis stays for the imaginary part of a complex number?
................................................................................................................................
Binoms
The binoms are not complete. To all in all the four signs of the two pairs of factors, which are built by a and b , there are altogether 16 permutations of the prefixes (signs) possible. To read up on the text `16 Permutationen´ (you may ask for it by e-mail address, lateron if necassary at the blog); usable by the sheet `Binomenfamilie´ (available like `16 Permutationen`).
Martinez quoted rules to built products in 'negative math' which are different to the classical algebra (beyond in red as result after `∨´). In the representation `Martinez A3´ on the one hand the three well known binoms, completed by that one new binoms which are different in result, are depicted and on the other hand the rules to the prefixes, so Martinez did, are coupled to be examinable. For to read up there is `Martinez A3´ (ask for it by e-mail, lateron if necassary at the blog), useable the sheet `Perm Martinez´ (available like `Martinez A3´).
(a − b) (a − b) = a² − 2ab + b² ∨ −a² + 2ab − b² ∀ a, b ∈ IR By `∨´ a contradiction is given! Which logical formulation will bring the solution? ................................................................................................................................
• ∀ ∃ ⊥ ∫ | ‰ ≤ ~ = ≠ ≡ ∨ Λ + ⋅ ∗ − : ÷ ⁄ √ Σ (Sigma - Summenmenge), Π (Pi - Produktmenge), Θ (Theta - Quotientmenge)
+ − ± ⋅ × ∗ : ÷ / < ≤ = ≠ ≡ ≥ > ∞ • 〈 〉 ¬ ∧ ∨ ⇔ ⇐ ⇒ ⊂ ∈ ⊄ ƒ |
|